AMC 8 – 1986 Problems (1986 AJHSME Problems)
Problem 1
In July 1861, $366$ inches of rain fell in Cherrapunji, India. What was the average rainfall in inches per hour during that month?
$\text{(A)}\ \frac{366}{31\times 24}$
$\text{(B)}\ \frac{366\times 31}{24}$
$\text{(C)}\ \frac{366\times 24}{31}$
$\text{(D)}\ \frac{31\times 24}{366}$
$\text{(E)}\ 366\times 31\times 24$
Problem 2
Which of the following numbers has the largest reciprocal?
$\text{(A)}\ \frac{1}{3} \qquad$
$\text{(B)}\ \frac{2}{5} \qquad$
$ \text{(C)}\ 1 \qquad $
$\text{(D)}\ 5 \qquad$
$ \text{(E)}\ 1986$
Problem 3
The smallest sum one could get by adding three different numbers from the set $\{ 7,25,-1,12,-3 \}$ is
$\text{(A)}\ -3 \qquad$
$ \text{(B)}\ -1 \qquad$
$ \text{(C)}\ 3 \qquad$
$ \text{(D)}\ 5 \qquad $
$\text{(E)}\ 21$
Problem 4
The product $(1.8)(40.3+.07)$ is closest to
$\text{(A)}\ 7 \qquad
$\text{(B)}\ 42 \qquad $
$\text{(C)}\ 74 \qquad $
$\text{(D)}\ 84 \qquad$
$\text{(E)}\ 737$
Problem 5
A contest began at noon one day and ended $1000$ minutes later. At what time did the contest end?
$\text{(A)}\ \text{10:00 p.m.} \qquad$
$ \text{(B)}\ \text{midnight} \qquad $
$\text{(C)}\ \text{2:30 a.m.} \qquad$
$ \text{(D)}\ \text{4:40 a.m.} \qquad$
$ \text{(E)}\ \text{6:40 a.m.}$
Problem 6
$\frac{2}{1-\frac{2}{3}}=$
$\text{(A)}\ -3 \qquad $
$\text{(B)}\ -\frac{4}{3} \qquad$
$ \text{(C)}\ \frac{2}{3} \qquad$
$ \text{(D)}\ 2 \qquad$
$ \text{(E)}\ 6$
Problem 7
How many whole numbers are between $\sqrt{8}$ and $\sqrt{80}$?
$\text{(A)}\ 5 \qquad$
$ \text{(B)}\ 6 \qquad $
$\text{(C)}\ 7 \qquad $
$\text{(D)}\ 8 \qquad$
$ \text{(E)}\ 9$
Problem 8
In the product shown, $\text{B}$ is a digit. The value of $\text{B}$ is
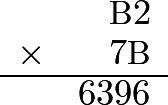
$\text{(A)}\ 3 \qquad $
$\text{(B)}\ 5 \qquad$
$ \text{(C)}\ 6 \qquad $
$\text{(D)}\ 7 \qquad $
$\text{(E)}\ 8$
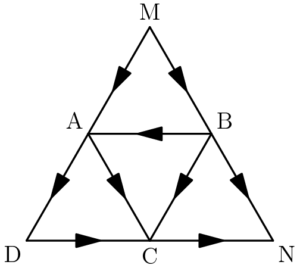
Problem 9
Using only the paths and the directions shown, how many different routes are there from $\text{M}$ to $\text{N}$?
$\text{(A)}\ 2 \qquad$
$ \text{(B)}\ 3 \qquad $
$\text{(C)}\ 4 \qquad $
$\text{(D)}\ 5 \qquad$
$ \text{(E)}\ 6$
Problem 10
A picture $3$ feet across is hung in the center of a wall that is $19$ feet wide. How many feet from the end of the wall is the nearest edge of the picture?
$\text{(A)}\ 1\frac{1}{2} \qquad$
$ \text{(B)}\ 8 \qquad $
$\text{(C)}\ 9\frac{1}{2} \qquad $
$\text{(D)}\ 16 \qquad $
$\text{(E)}\ 22$
Problem 11
If $\text{A}*\text{B}$ means $\frac{\text{A}+\text{B}}{2}$, then $(3*5)*8$ is
$\text{(A)}\ 6 \qquad $
$\text{(B)}\ 8 \qquad$
$ \text{(C)}\ 12 \qquad $
$\text{(D)}\ 16\qquad$
$ \text{(E)}\ 30$
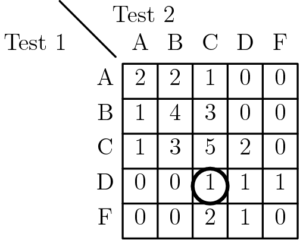
Problem 12
The table below displays the grade distribution of the $30$ students in a mathematics class on the last two tests. For example, exactly one student received a ‘D’ on Test 1 and a ‘C’ on Test 2 (see circled entry). What percent of the students received the same grade on both tests?
$\text{(A)}\ 12\% \qquad$
$ \text{(B)}\ 25\% \qquad$
$ \text{(C)}\ 33\frac{1}{3}\% \qquad$
$ \text{(D)}\ 40\% \qquad$
$ \text{(E)}\ 50\%$
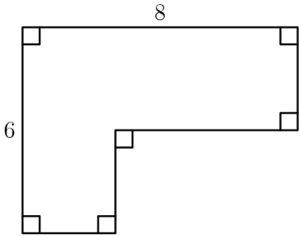
Problem 13
The perimeter of the polygon shown is
$\text{(A)}\ 14 \qquad$
$ \text{(B)}\ 20 \qquad$
$ \text{(C)}\ 28 \qquad$
$ \text{(D)}\ 48$
$\text{(E)}\ \text{cannot be determined from the information given}$
Problem 14
If $200\leq a \leq 400$ and $600\leq b\leq 1200$, then the largest value of the quotient $\frac{b}{a}$ is
$\text{(A)}\ \frac{3}{2} \qquad$
$ \text{(B)}\ 3 \qquad$
$ \text{(C)}\ 6 \qquad$
$ \text{(D)}\ 300 \qquad$
$ \text{(E)}\ 600$
Problem 15
Sale prices at the Ajax Outlet Store are $50\%$ below original prices. On Saturdays an additional discount of $20\%$ off the sale price is given. What is the Saturday price of a coat whose original price is $$180$?
$\text{(A)}$ $$54$
$\text{(B)}$ $$72$
$\text{(C)}$ $$90$
$\text{(D)}$ $$108$
$\text{(D)}$ $$110$
Problem 16
A bar graph shows the number of hamburgers sold by a fast food chain each season. However, the bar indicating the number sold during the winter is covered by a smudge. If exactly $25\%$ of the chain’s hamburgers are sold in the fall, how many million hamburgers are sold in the winter?
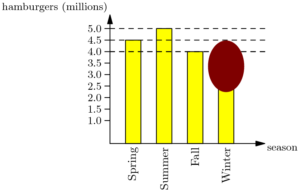$\text{(A)}\ 2.5 \qquad $
$\text{(B)}\ 3 \qquad$
$ \text{(C)}\ 3.5 \qquad$
$ \text{(D)}\ 4 \qquad $
$\text{(E)}\ 4.5$
Problem 17
Let $\text{o}$ be an odd whole number and let $\text{n}$ be any whole number. Which of the following statements about the whole number $(\text{o}^2+\text{no})$ is always true?
$\text{(A)}\ \text{it is always odd} \qquad$
$ \text{(B)}\ \text{it is always even}$
$\text{(C)}\ \text{it is even only if n is even} \qquad $
$\text{(D)}\ \text{it is odd only if n is odd}$
$\text{(E)}\ \text{it is odd only if n is even}$
Problem 18
A rectangular grazing area is to be fenced off on three sides using part of a $100$ meter rock wall as the fourth side. Fence posts are to be placed every $12$ meters along the fence including the two posts where the fence meets the rock wall. What is the fewest number of posts required to fence an area $36$ m by $60$ m?
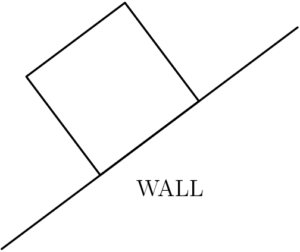
$\text{(A)}\ 11 \qquad $
$\text{(B)}\ 12 \qquad$
$ \text{(C)}\ 13 \qquad$
$ \text{(D)}\ 14 \qquad$
$ \text{(E)}\ 16$
Problem 19
At the beginning of a trip, the mileage odometer read $56,200$ miles. The driver filled the gas tank with $6$ gallons of gasoline. During the trip, the driver filled his tank again with $12$ gallons of gasoline when the odometer read $56,560$. At the end of the trip, the driver filled his tank again with $20$ gallons of gasoline. The odometer read $57,060$. To the nearest tenth, what was the car’s average miles-per-gallon for the entire trip?
$\text{(A)}\ 22.5 \qquad$
$ \text{(B)}\ 22.6 \qquad$
$\text{(C)}\ 24.0 \qquad$
$ \text{(D)}\ 26.9 \qquad $
$\text{(E)}\ 27.5$
Problem 20
The value of the expression $\frac{(304)^5}{(29.7)(399)^4}$ is closest to
$\text{(A)}\ .003 \qquad$
$ \text{(B)}\ .03 \qquad
$ \text{(C)}\ .3 \qquad $
$\text{(D)}\ 3 \qquad$
$ \text{(E)}\ 30$
Problem 21
Suppose one of the eight lettered identical squares is included with the four squares in the T-shaped figure outlined. How many of the resulting figures can be folded into a topless cubical box?
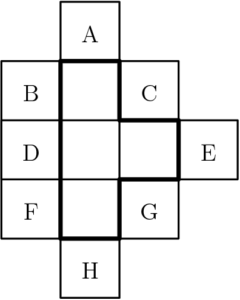
$\text{(A)}\ 2 \qquad$
$ \text{(B)}\ 3 \qquad$
$ \text{(C)}\ 4 \qquad $
$\text{(D)}\ 5 \qquad $
$\text{(E)}\ 6$
Problem 22
Alan, Beth, Carlos, and Diana were discussing their possible grades in mathematics class this grading period. Alan said, “If I get an A, then Beth will get an A.” Beth said, “If I get an A, then Carlos will get an A.” Carlos said, “If I get an A, then Diana will get an A.” All of these statements were true, but only two of the students received an A. Which two received A’s?
$\text{(A)}\ \text{Alan, Beth} \qquad$
$ \text{(B)}\ \text{Beth, Carlos} \qquad$
$ \text{(C)}\ \text{Carlos, Diana}$
$\text{(D)}\ \text{Alan, Diana} \qquad$
$ \text{(E)}\ \text{Beth, Diana}$
Problem 23
The large circle has diameter $\text{AC}$. The two small circles have their centers on $\text{AC}$ and just touch at $\text{O}$, the center of the large circle. If each small circle has radius $1$, what is the value of the ratio of the area of the shaded region to the area of one of the small circles?
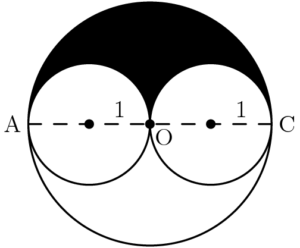
$\text{(A)}\ \text{between }\frac{1}{2}\text{ and 1} \qquad $
$\text{(B)}\ 1 \qquad$
$ \text{(C)}\ \text{between 1 and }\frac{3}{2}$
$\text{(D)}\ \text{between }\frac{3}{2}\text{ and 2} \qquad $
$\text{(E)}\ \text{cannot be determined from the information given}$
Problem 24
The $600$ students at King Middle School are divided into three groups of equal size for lunch. Each group has lunch at a different time. A computer randomly assigns each student to one of three lunch groups. The probability that three friends, Al, Bob, and Carol, will be assigned to the same lunch group is approximately
$\text{(A)}\ \frac{1}{27} \qquad$
$ \text{(B)}\ \frac{1}{9} \qquad$
$ \text{(C)}\ \frac{1}{8} \qquad $
$\text{(D)}\ \frac{1}{6} \qquad $
$\text{(E)}\ \frac{1}{3}$
Problem 25
Which of the following sets of whole numbers has the largest average?
$\text{(A)}\ \text{multiples of 2 between 1 and 101} \qquad $
$\text{(B)}\ \text{multiples of 3 between 1 and 101}$
$\text{(C)}\ \text{multiples of 4 between 1 and 101} \qquad $
$\text{(D)}\ \text{multiples of 5 between 1 and 101}$
$\text{(E)}\ \text{multiples of 6 between 1 and 101}$
