AMC 8 – 1987 Problems

AMC 8 – 1987 Problems (1987 AJHSME Problems)

Problem 1

$.4+.02+.006=$

$\text{(A)}\ .012 \qquad $

$\text{(B)}\ .066 \qquad$

$\text{(C)}\ .12 \qquad $

$\text{(D)}\ .24 \qquad$

$ \text{(E)} .426$

Problem 2

$\frac{2}{25}=$

$\text{(A)}\ .008 \qquad$

$\text{(B)}\ .08 \qquad$

$\text{(C)}\ .8 \qquad$

$\text{(D)} 1.25 \qquad$

$\text{(E)}\ 12.5$

Problem 3

$2(81+83+85+87+89+91+93+95+97+99)=$

$\text{(A)}\ 1600 \qquad$

$\text{(B)}\ 1650 \qquad$

$\text{(C)}\ 1700 \qquad$

$\text{(D)}\ 1750 \qquad$

$\text{(E)}\ 1800$

Problem 4

Martians measure angles in clerts. There are $500$ clerts in a full circle. How many clerts are there in a right angle?

$\text{(A)}\ 90 \qquad$

$\text{(B)}\ 100 \qquad$

$\text{(C)}\ 125 \qquad$

$\text{(D)}\ 180 \qquad$

$\text{(E)}\ 250$

Problem 5

The area of the rectangular region is

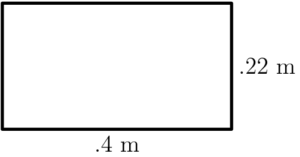
$\text{(A)}\ \text{.088 m}^2 \qquad$

$\text{(B)}\ \text{.62 m}^2 \qquad$

$\text{(C)}\ \text{.88 m}^2 \qquad$

$\text{(D)}\ \text{1.24 m}^2 \qquad$

$\text{(E)}\ \text{4.22 m}^2$

Problem 6

The smallest product one could obtain by multiplying two numbers in the set $\{ -7, -5, -1, 1, 3 \}$ is

$\text{(A)}\ -35 \qquad$

$ \text{(B)}\ -21 \qquad$

$ \text{(C)}\ -15 \qquad$

$ \text{(D)}\ -1 \qquad$

$ \text{(E)}\ 3$

Problem 7

The large cube shown is made up of $27$ identical sized smaller cubes. For each face of the large cube, the opposite face is shaded the same way. The total number of smaller cubes that must have at least one face shaded is

$\text{(A)}\ 10 \qquad$

$\text{(B)}\ 16 \qquad$

$\text{(C)}\ 20 \qquad$

$\text{(D)}\ 22 \qquad$

$\text{(E)}\ 24$

 

Problem 8

If $\text{A}$ and $\text{B}$ are nonzero digits, then the number of digits (not necessarily different) in the sum of the three whole numbers is

$\text{(A)}\ 4 \qquad$

$\text{(B)}\ 5 \qquad$

$\text{(C)}\ 6 \qquad$

$\text{(D)}\ 9 \qquad$

$\text{(E)}\ \text{depends on the values of A and B}$

Problem 9

When finding the sum $\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+\frac{1}{7}$, the least common denominator used is

$\text{(A)}\ 120 \qquad$

$\text{(B)}\ 210 \qquad$

$\text{(C)}\ 420 \qquad$

$\text{(D)}\ 840 \qquad$

$\text{(E)}\ 5040$

Problem 10

$4(299)+3(299)+2(299)+298=$

$\text{(A)}\ 2889 \qquad$

$\text{(B)}\ 2989 \qquad$

$\text{(C)}\ 2991 \qquad$

$\text{(D)}\ 2999 \qquad$

$ \text{(E)}\ 3009$

Problem 11

The sum $2\frac17+3\frac12+5\frac{1}{19}$ is between

$\text{(A)}\ 10\text{ and }10\frac12 \qquad$

$\text{(B)}\ 10\frac12 \text{ and } 11 \qquad$

$\text{(C)}\ 11\text{ and }11\frac12 \qquad$

$\text{(D)}\ 11\frac12 \text{ and }12 \qquad$

$\text{(E)}\ 12\text{ and }12\frac12$

Problem 12

What fraction of the large $12$ by $18$ rectangular region is shaded?

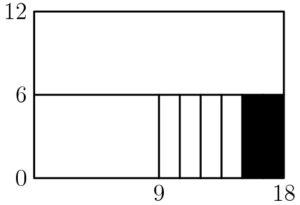
$\text{(A)}\ \frac{1}{108} \qquad$

$\text{(B)}\ \frac{1}{18} \qquad$

$\text{(C)}\ \frac{1}{12} \qquad$

$\text{(D)}\ \frac29 \qquad$

$ \text{(E)}\ \frac13$

Problem 13

Which of the following fractions has the largest value?

$\text{(A)}\ \frac{3}{7} \qquad$

$\text{(B)}\ \frac{4}{9} \qquad$

$\text{(C)}\ \frac{17}{35} \qquad$

$\text{(D)}\ \frac{100}{201}\qquad$

$ \text{(E)}\ \frac{151}{301}$

Problem 14

A computer can do $10,000$ additions per second. How many additions can it do in one hour?

$\text{(A)}\ 6\text{ million} \qquad$

$\text{(B)}\ 36\text{ million} \qquad$

$\text{(C)}\ 60\text{ million} \qquad$

$\text{(D)}\ 216\text{ million} \qquad$

$\text{(E)}\ 360\text{ million}$

Problem 15

The sale ad read: “Buy three tires at the regular price and get the fourth tire for three dollars;.” Sam paid $240\text{ dollars}$ for a set of four tires at the sale. What was the regular price of one tire?

$\text{(A)}\ 59.25\text{ dollars} \qquad$

$\text{(B)}\ 60\text{ dollars} \qquad$

$\text{(C)}\ 70\text{ dollars} \qquad$

$\text{(D)}\ 79\text{ dollars} \qquad$

$ \text{(E)}\ 80\text{ dollars}$

Problem 16

Joyce made $12$ of her first $30$ shots in the first three games of this basketball game, so her seasonal shooting average was $40\%$. In her next game, she took $10$ shots and raised her seasonal shooting average to $50\%$. How many of these $10$ shots did she make?

$\text{(A)}\ 2 \qquad$

$\text{(B)}\ 3 \qquad$

$\text{(C)}\ 5 \qquad$

$\text{(D)}\ 6 \qquad$

$ \text{(E)}\ 8$

Problem 17

Abby, Bret, Carl, and Dana are seated in a row of four seats numbered #1 to #4. Joe looks at them and says:

“Bret is next to Carl.”
“Abby is between Bret and Carl.”
However each one of Joe’s statements is false. Bret is actually sitting in seat #3. Who is sitting in seat #2?

$\text{(A)}\ \text{Abby} \qquad

\text{(B)}\ \text{Bret} \qquad

\text{(C)}\ \text{Carl} \qquad

\text{(D)}\ \text{Dana} \qquad

\text{(E)}\ \text{There is not enough information to be sure.}$

Problem 18

Half the people in a room left. One third of those remaining started to dance. There were then $12$ people who were not dancing. The original number of people in the room was what?

$\text{(A)}\ 24 \qquad

\text{(B)}\ 30 \qquad

\text{(C)}\ 36 \qquad

\text{(D)}\ 42 \qquad

\text{(E)}\ 72$

Problem 19

A calculator has a squaring key $\boxed{x^2}$ which replaces the current number displayed with its square. For example, if the display is $\boxed{000003}$ and the $\boxed{x^2}$ key is depressed, then the display becomes $\boxed{000009}$. If the display reads $\boxed{000002}$, how many times must you depress the $\boxed{x^2}$ key to produce a displayed number greater than $500$?

$\text{(A)}\ 4 \qquad$

$\text{(B)}\ 5 \qquad$

$\text{(C)}\ 8 \qquad$

$\text{(D)}\ 9 \qquad$

$\text{(E)}\ 250$

Problem 20

“If a whole number $n$ is not prime, then the whole number $n-2$ is not prime.” A value of $n$ which shows this statement to be false is

$\text{(A)}\ 9 \qquad$

$\text{(B)}\ 12 \qquad$

$\text{(C)}\ 13 \qquad$

$\text{(D)}\ 16 \qquad$

$ \text{(E)}\ 23$

Problem 21

Suppose $n^{*}$ means $\frac{1}{n}$, the reciprocal of $n$. For example, $5^{*}=\frac{1}{5}$. How many of the following statements are true?

i) $3^*+6^*=9^*$
ii) $6^*-4^*=2^*$
iii) $2^*\cdot 6^*=12^*$
iv) $10^*\div 2^* =5^*$
$\text{(A)}\ 0 \qquad$

$\text{(B)}\ 1 \qquad$

$\text{(C)}\ 2 \qquad$

$\text{(D)}\ 3 \qquad$

$\text{(E)}\ 4$

Problem 22

$\text{ABCD}$ is a rectangle, $\text{D}$ is the center of the circle, and $\text{B}$ is on the circle. If $\text{AD}=4$ and $\text{CD}=3$, then the area of the shaded region is between

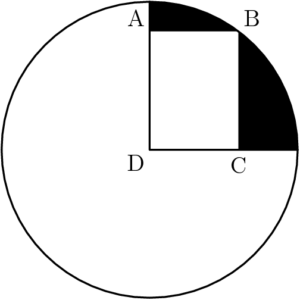
$\text{(A)}\ 4\text{ and }5 \qquad$

$\text{(B)}\ 5\text{ and }6 \qquad$

$\text{(C)}\ 6\text{ and }7 \qquad$

$\text{(D)}\ 7\text{ and }8 \qquad$

$\text{(E)}\ 8\text{ and }9$

Problem 23

Assume the adjoining chart shows the $1980$ U.S. population, in millions, for each region by ethnic group. To the nearest percent, what percent of the U.S. Black population lived in the South?

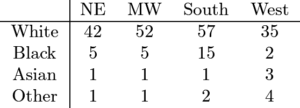
$\text{(A)}\ 20\% \qquad$

$\text{(B)}\ 25\% \qquad$

$\text{(C)}\ 40\% \qquad$

$\text{(D)}\ 56\% \qquad$

$\text{(E)}\ 80\%$

Problem 24

Problem 24
A multiple choice examination consists of $20$ questions. The scoring is $+5$ for each correct answer, $-2$ for each incorrect answer, and $0$ for each unanswered question. John’s score on the examination is $48$. What is the maximum number of questions he could have answered correctly?

$\text{(A)}\ 9 \qquad$

$\text{(B)}\ 10 \qquad$

$\text{(C)}\ 11 \qquad$

$\text{(D)}\ 12 \qquad$

$\text{(E)}\ 16$

Problem 25

Ten balls numbered $1$ to $10$ are in a jar. Jack reaches into the jar and randomly removes one of the balls. Then Jill reaches into the jar and randomly removes a different ball. The probability that the sum of the two numbers on the balls removed is even is

$\text{(A)}\ \frac{4}{9} \qquad$

$\text{(B)}\ \frac{9}{19} \qquad$

$\text{(C)}\ \frac{1}{2} \qquad$

$\text{(D)}\ \frac{10}{19} \qquad$

$\text{(E)}\ \frac{5}{9}$