AMC 8 – 1989 Problems (1989 AJHSME Problems)
Problem 1
$(1+11+21+31+41)+(9+19+29+39+49)=$
$\text{(A)}\ 150 \qquad$
$\text{(B)}\ 199 \qquad$
$\text{(C)}\ 200 \qquad$
$\text{(D)}\ 249 \qquad$
$\text{(E)}\ 250$
Problem 2
$\frac{2}{10}+\frac{4}{100}+\frac{6}{1000} =$
$\text{(A)}\ .012 \qquad$
$ \text{(B)}\ .0246 \qquad$
$ \text{(C)}\ .12 \qquad$
$ \text{(D)}\ .246 \qquad$
$ \text{(E)}\ 246$
Problem 3
Which of the following numbers is the largest?
$\text{(A)}\ .99 \qquad $
$\text{(B)}\ .9099 \qquad $
$\text{(C)}\ .9 \qquad $
$\text{(D)}\ .909 \qquad$
$ \text{(E)}\ .9009$
Problem 4
Estimate to determine which of the following numbers is closest to $\frac{401}{.205}$.
$\text{(A)}\ .2 \qquad$
$ \text{(B)}\ 2 \qquad$
$ \text{(C)}\ 20 \qquad$
$ \text{(D)}\ 200 \qquad $
$\text{(E)}\ 2000$
Problem 5
$-15+9\times (6\div 3) =$
$\text{(A)}\ -48 \qquad$
$ \text{(B)}\ -12 \qquad $
$\text{(C)}\ -3 \qquad$
$ \text{(D)}\ 3 \qquad $
$\text{(E)}\ 12$
Problem 6
If the markings on the number line are equally spaced, what is the number $\text{y}$?
$\text{(A)}\ 3 \qquad$
$ \text{(B)}\ 10 \qquad$
$ \text{(C)}\ 12 \qquad$
$ \text{(D)}\ 15 \qquad$
$ \text{(E)}\ 16$
Problem 7
If the value of $20$ quarters and $10$ dimes equals the value of $10$ quarters and $n$ dimes, then $n=$
$\text{(A)}\ 10 \qquad$
$ \text{(B)}\ 20 \qquad $
$\text{(C)}\ 30 \qquad$
$ \text{(D)}\ 35 \qquad$
$ \text{(E)}\ 45$
Problem 8
$(2\times 3\times 4)\left(\frac{1}{2}+\frac{1}{3}+\frac{1}{4}\right) =$
$\text{(A)}\ 1 \qquad$
$ \text{(B)}\ 3 \qquad $
$\text{(C)}\ 9 \qquad$
$ \text{(D)}\ 24 \qquad$
$ \text{(E)}\ 26$
Problem 9
There are $2$ boys for every $3$ girls in Ms. Johnson’s math class. If there are $30$ students in her class, what percent of them are boys?
$\text{(A)}\ 12\% \qquad$
$ \text{(B)}\ 20\% \qquad $
$\text{(C)}\ 40\% \qquad$
$ \text{(D)}\ 60\% \qquad$
$ \text{(E)}\ 66\frac{2}{3}\%$
Problem 10
What is the number of degrees in the smaller angle between the hour hand and the minute hand on a clock that reads seven o’clock?
$\text{(A)}\ 50^\circ \qquad $
$\text{(B)}\ 120^\circ \qquad$
$ \text{(C)}\ 135^\circ \qquad$
$ \text{(D)}\ 150^\circ \qquad$
$ \text{(E)}\ 165^\circ$
Problem 11
Which of the five “T-like shapes” would be symmetric to the one shown with respect to the dashed line?
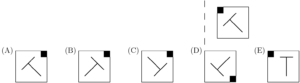Problem 12
$\frac{1-\frac{1}{3}}{1-\frac{1}{2}} =$
$\text{(A)}\ \frac{1}{3} \qquad$
$ \text{(B)}\ \frac{2}{3} \qquad$
$ \text{(C)}\ \frac{3}{4} \qquad$
$ \text{(D)}\ \frac{3}{2} \qquad $
$\text{(E)}\ \frac{4}{3}$
Problem 13
$\frac{9}{7\times 53} =$
$\text{(A)}\ \frac{.9}{.7\times 53} \qquad$
$ \text{(B)}\ \frac{.9}{.7\times .53} \qquad$
$ \text{(C)}\ \frac{.9}{.7\times 5.3} \qquad$
$ \text{(D)}\ \frac{.9}{7\times .53} \qquad$
$ \text{(E)}\ \frac{.09}{.07\times .53}$
Problem 14
When placing each of the digits $2,4,5,6,9$ in exactly one of the boxes of this subtraction problem, what is the smallest difference that is possible?
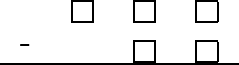
$\text{(A)}\ 58 \qquad $
$\text{(B)}\ 123 \qquad$
$ \text{(C)}\ 149 \qquad$
$ \text{(D)}\ 171 \qquad$
$ \text{(E)}\ 176$
$text{(E)} 37$
Problem 15
The area of the shaded region $\text{BEDC}$ in parallelogram $\text{ABCD}$ is
$\text{(A)}\ 24 \qquad$
$ \text{(B)}\ 48 \qquad $
$\text{(C)}\ 60 \qquad $
$\text{(D)}\ 64 \qquad $
$\text{(E)}\ 80$
Problem 16
In how many ways can $47$ be written as the sum of two primes?
$\text{(A)}\ 0 \qquad$
$ \text{(B)}\ 1 \qquad $
$\text{(C)}\ 2 \qquad$
$ \text{(D)}\ 3 \qquad$
$ \text{(E)}\ \text{more than 3}$
Problem 17
The number $\text{N}$ is between $9$ and $17$. The average of $6$, $10$, and $\text{N}$ could be
$\text{(A)}\ 8 \qquad$
$ \text{(B)}\ 10 \qquad $
$\text{(C)}\ 12 \qquad $
$\text{(D)}\ 14 \qquad$
$ \text{(E)}\ 16$
Problem 18
Many calculators have a reciprocal key $\boxed{\frac{1}{x}}$ that replaces the current number displayed with its reciprocal. For example, if the display is $\boxed{00004}$ and the $\boxed{\frac{1}{x}}$ key is pressed, then the display becomes $\boxed{000.25}$. If $\boxed{00032}$ is currently displayed, what is the fewest positive number of times you must depress the $\boxed{\frac{1}{x}}$ key so the display again reads $\boxed{00032}$?
$\text{(A)}\ 1 \qquad$
$ \text{(B)}\ 2 \qquad$
$ \text{(C)}\ 3 \qquad$
$ \text{(D)}\ 4 \qquad $
$\text{(E)}\ 5$
Problem 19
The graph below shows the total accumulated dollars (in millions) spent by the Surf City government during $1988$. For example, about $.5$ million had been spent by the beginning of February and approximately $2$ million by the end of April. Approximately how many millions of dollars were spent during the summer months of June, July, and August?
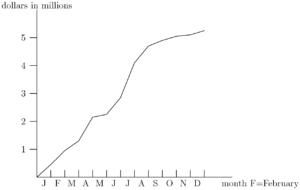
$\text{(A)}\ 1.5 \qquad$
$ \text{(B)}\ 2.5 \qquad$
$ \text{(C)}\ 3.5 \qquad$
$ \text{(D)}\ 4.5 \qquad$
$ \text{(E)}\ 5.5$
Problem 20
The figure may be folded along the lines shown to form a number cube. Three number faces come together at each corner of the cube. What is the largest sum of three numbers whose faces come together at a corner?
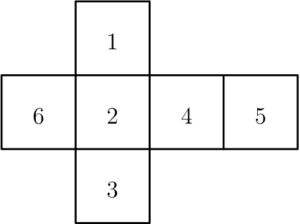
$\text{(A)}\ 11 \qquad \text{(B)}\ 12 \qquad \text{(C)}\ 13 \qquad \text{(D)}\ 14 \qquad \text{(E)}\ 15$
Problem 21
Jack had a bag of $128$ apples. He sold $25\%$ of them to Jill. Next he sold $25\%$ of those remaining to June. Of those apples still in his bag, he gave the shiniest one to his teacher. How many apples did Jack have then?
$\text{(A)}\ 7 \qquad$
$ \text{(B)}\ 63 \qquad$
$ \text{(C)}\ 65 \qquad$
$ \text{(D)}\ 71 \qquad$
$ \text{(E)}\ 111$
Problem 22
The letters $\text{A}$, $\text{J}$, $\text{H}$, $\text{S}$, $\text{M}$, $\text{E}$ and the digits $1$, $9$, $8$, $9$ are “cycled” separately as follows and put together in a numbered list:
What is the number of the line on which $\text{AJHSME 1989}$ will appear for the first time?
$\text{(A)}\ 6 \qquad$
$ \text{(B)}\ 10 \qquad$
$ \text{(C)}\ 12 \qquad$
$ \text{(D)}\ 18 \qquad$
$ \text{(E)}\ 24$
Problem 23
An artist has $14$ cubes, each with an edge of $1$ meter. She stands them on the ground to form a sculpture as shown. She then paints the exposed surface of the sculpture. How many square meters does she paint?
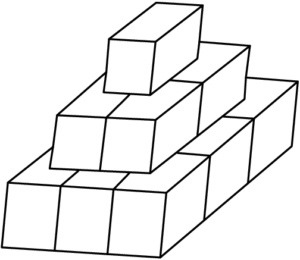
$\text{(A)}\ 21 \qquad$
$ \text{(B)}\ 24 \qquad$
$ \text{(C)}\ 33 \qquad$
$ \text{(D)}\ 37 \qquad$
$ \text{(E)}\ 42$
Problem 24
Suppose a square piece of paper is folded in half vertically. The folded paper is then cut in half along the dashed line. Three rectangles are formed-a large one and two small ones. What is the ratio of the perimeter of one of the small rectangles to the perimeter of the large rectangle?
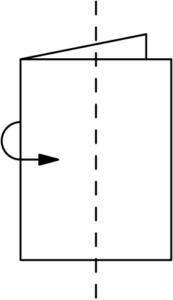
$\text{(A)}\ \frac{1}{2} \qquad $
$\text{(B)}\ \frac{2}{3} \qquad$
$ \text{(C)}\ \frac{3}{4} \qquad $
$\text{(D)}\ \frac{4}{5} \qquad$
$ \text{(E)}\ \frac{5}{6}$
Problem 25
Every time these two wheels are spun, two numbers are selected by the pointers. What is the probability that the sum of the two selected numbers is even?
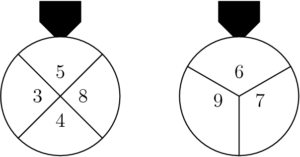
$\text{(A)}\ \frac{1}{6} \qquad$
$ \text{(B)}\ \frac{3}{7} \qquad $
$\text{(C)}\ \frac{1}{2} \qquad$
$ \text{(D)}\ \frac{2}{3} \qquad$
$ \text{(E)}\ \frac{5}{7}$
